Elastica®
Die Software für kontaktmechanische Berechnung
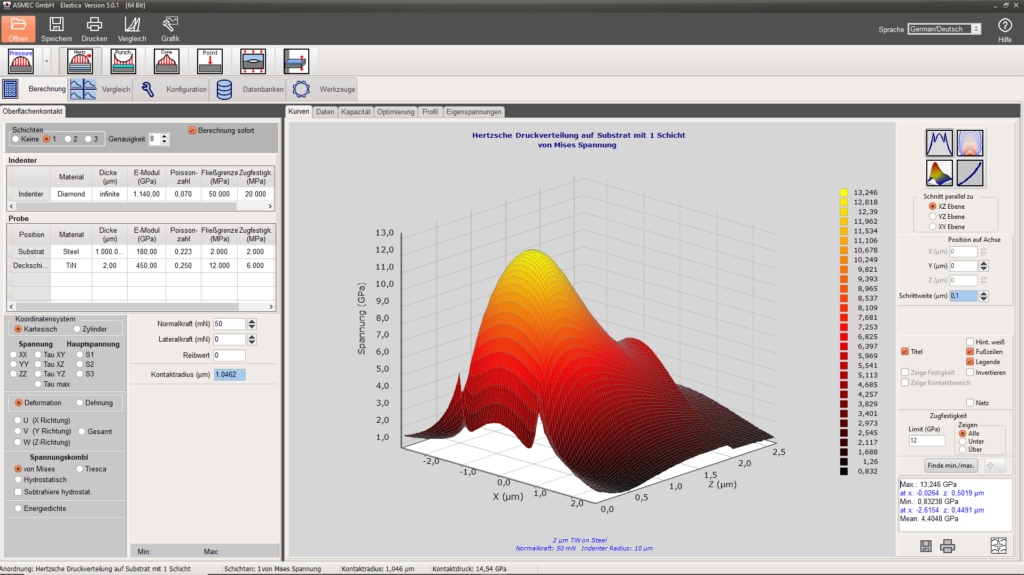
Die Elastica Software präsentiert kontaktmechanische Lösungen für rein elastischen Kontakt oder elastische Deformationen in einer einfachen, benutzerfreundlichen und sehr schnellen Form (keine Finite Elemente Methode). Sie ist hauptsächlich für die Untersuchung von Oberflächenkontakten entwickelt, enthält aber auch ein Modul zur Berechnung der Resonanzfrequenzen schwingender Cantilever.
Es gibt Lösungen für Kugeln, Kegel oder flache Stempel als Indenter und Punktkräfte wobei nur die Kugelindenter von praktischer Bedeutung sind
Wesentliche Anwendungen von Elastica
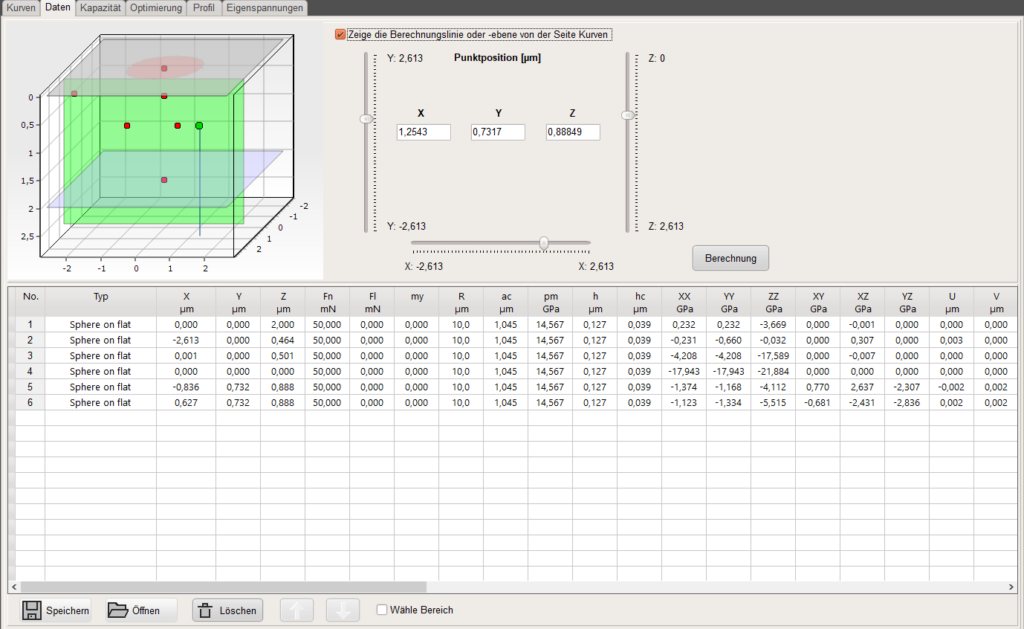
- Untersuchung von elastischen Spannungs-, Dehnungs- oder Deformationsfeldern für beschichtete Materialien unter statischer Kraft- oder Stoßeinwirkung (Normal− und Lateralkräfte)
- Schnelle Abschätzung der lasttragenden Kapazität von beschichteten Oberflächen
- Optimierung von Beschichtungen zum mechanischen Schutz und Unterstützung beim Schichtsystemdesign
- Auswertung von Eindruck−, Scratch− oder Verschleißtests und Unterstützung bei Entwurf und Durchführung solcher Tests
- Auswertung des Einflusses von Oberflächenprofilen (Rauheit) auf die lokalen Spannungen und Deformationen
- Berechnung der Resonanzfrequenzen beschichteter oder unbeschichteter Cantilever
Vorteile von Elastica im Vergleich mit Finite Element und Boundary Element Berechnungen
- Die Rechnungen sind durch die Nutzung komplett analytischer Lösungen der Kontaktprobleme ungefähr 1000−mal schneller als FE Rechnungen. Dies ermöglicht erstmals eine vollständige Variation aller Parameter und deren Optimierung.
- Scharfe Spannungsspitzen und die Position und die Ausmaße der Kontaktfläche können genau berechnet und dargestellt werden.
- Bis zu 3 Schichten auf einem Substrat mit Dicken zwischen einigen Nanometern und mehreren Metern können ohne Neudesign der Kontaktgeometrie untersucht werden.
- Nicht−rotationssymmetrische Kontaktprobleme, verursacht durch das Wirken von Tangentialkräften, können mit der gleichen, hohen Rechengeschwindigkeit untersucht werden.
Die wichtigsten Annahmen des Modells
- Ideal glatte Grenz− und Oberflächen
- Homogene und isotrope Materialien
- Ideale Adhäsion der Schichten
Für viele der untersuchten praktischen Probleme sind die Modellannahmen viel weniger einschränkend als oft befürchtet. Trotz der Idealisierungen liefert das Modell in den meisten Fällen sehr brauchbare Ergebnisse. Wenn Sie sich nicht sicher sind ob Ihr kontaktmechanisches Problem mit Elastica simuliert werden kann, kontaktieren Sie uns, wir helfen Ihnen gern.
Nutzen der Reiter
Auf der Daten-Seite können die Ergebnisse für verschiedene Positionen in einer Tabelle gesammelt werden. Die obere linke Grafik stellt den Rechenbereich dar, der in der Konfiguration festgelegt wird. Der rote Kreis um die Position (0,0,0) gibt die Größe der Kontaktfläche an.
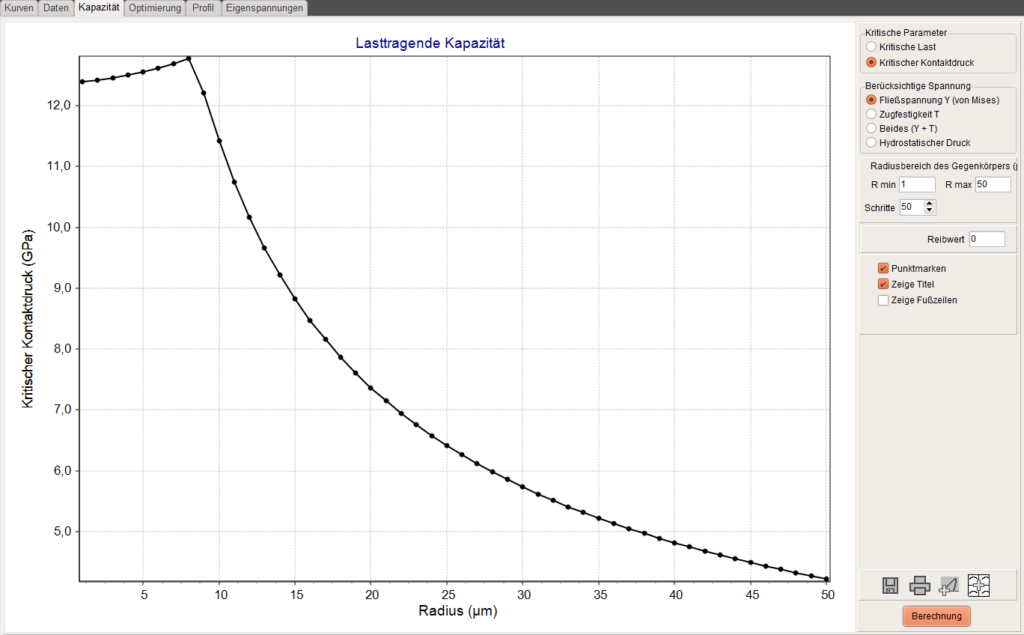
Diese Seite erlaubt eine schnelle Berechnung der lasttragenden Kapazität von beschichteten und unbeschichteten Materialien in Abhängigkeit von den elastischen Eigenschaften, Streckgrenze, Zugfestigkeit und dem Radius das Gegenkörpers. Dies funktioniert ausschließlich bei kugelförmigen Gegenkörpern. Die Kraft, die erforderlich ist eine von Mises Spannung oder eine Zugspannung zu erzeugen, die gleich der Streckgrenze oder der Zugfestigkeit des Materials ist, wird als kritische Kraft bezeichnet.
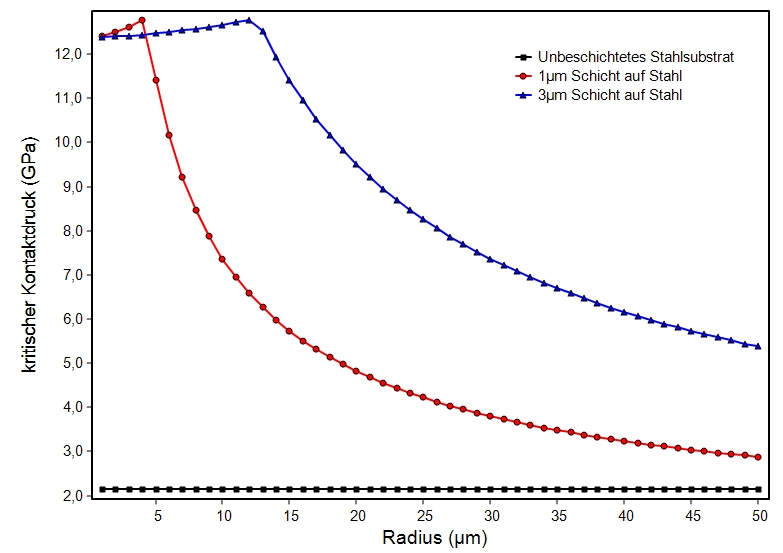
Bei Schichten hängt die lasttragende Kapazität stark vom Radius des Gegenkörpers ab. Die Schutzwirkung einer Schicht reicht nur bis zu einem maximalen Radius.
Die Grafik verdeutlicht die Bedeutung einer harten Schicht für die Lasttragfähigkeit einer Oberfläche und den Einfluss der Schichtdicke. Die Vergrößerung der Schichtdocke von 1µm auf 3µm hat einen drastischen Einfluss auf die Schutzwirkung der Schicht.
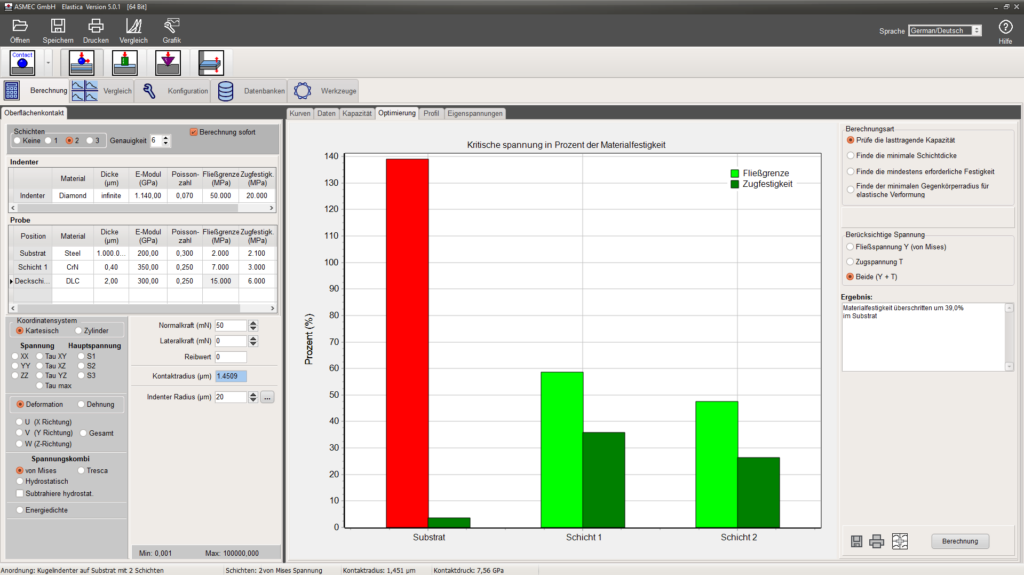
Diese Seite gibt einen schnellen Überblick ob die Festigkeitsgrenzen in einem Schichtsystem hoch genug sind, um einer bestimmten Belastung zu widerstehen. In der Grafik wird das für ein Doppelschichtsystem und einen Indenter mit 20µm Radius für eine Kraft von 50mN gezeigt. Es wird sichtbar, dass bei einer 2µm dicken Deckschicht die Härte das Stahlsubstrats nicht ausreicht, um der Belastung zu widerstehen. Der Fehlermechanismus wird plastische Verformung und keine Rissbildung sein.
Der rote und die hellgrünen Balken zeigen wie dicht (in Prozent) der maximale von Mises Stress an die Fließgrenze heranreicht, während die dunkelgrünen Balken das für die Zugfestigkeit zeigen. Wenn die Spannungswerte mehr als 100% der Festigkeit erreichen, werden die Balken rot.
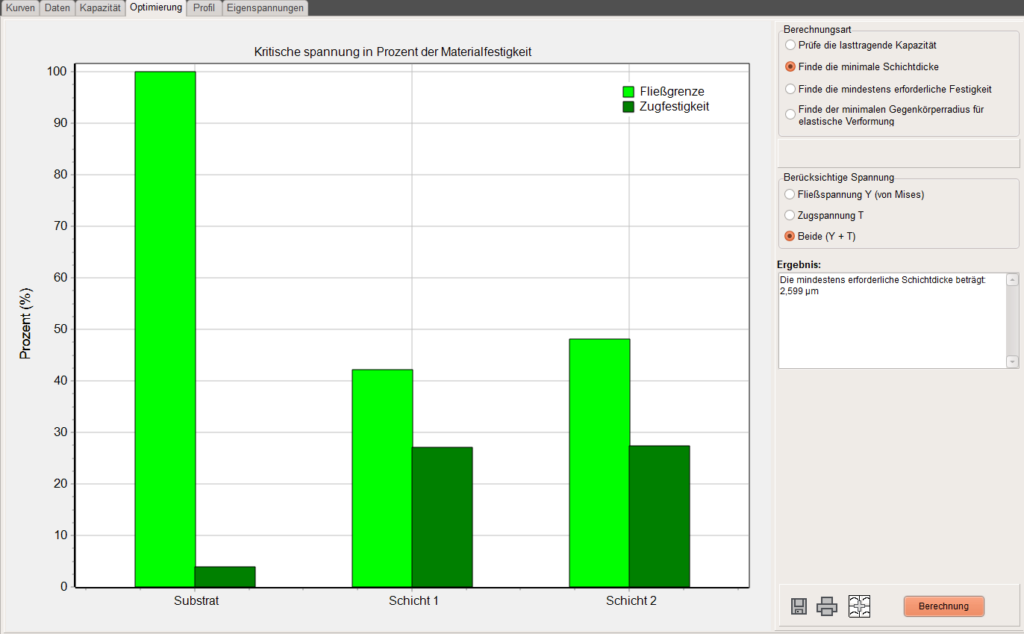
Wenn einer der Balken rot ist, kann man die Mindest-Schichtdicke bestimmen, ab der das Substrat geschützt wird, so dass keine der Spannungen die Materialfestigkeit überschreitet. In dem gegebenen Beispiel ist dies eine Schichtdicke von 2,608 µm.
Alternativ können auch die Mindestfestigkeit für alle Materialien des Schichtstapels oder der Mindestradius des Gegenkörpers für rein elastische Deformation berechnet werden.
Auf der Profilseite kann eine Datei mit einem Oberflächenprofil eingelesen werden, um die Spannungen, Dehnungen oder Deformationen entlang der Oberfläche in Abhängigkeit von der Position and den mechanischen Materialeigenschaften von bis zu drei Schichten auf einem Substrat zu berechnen.
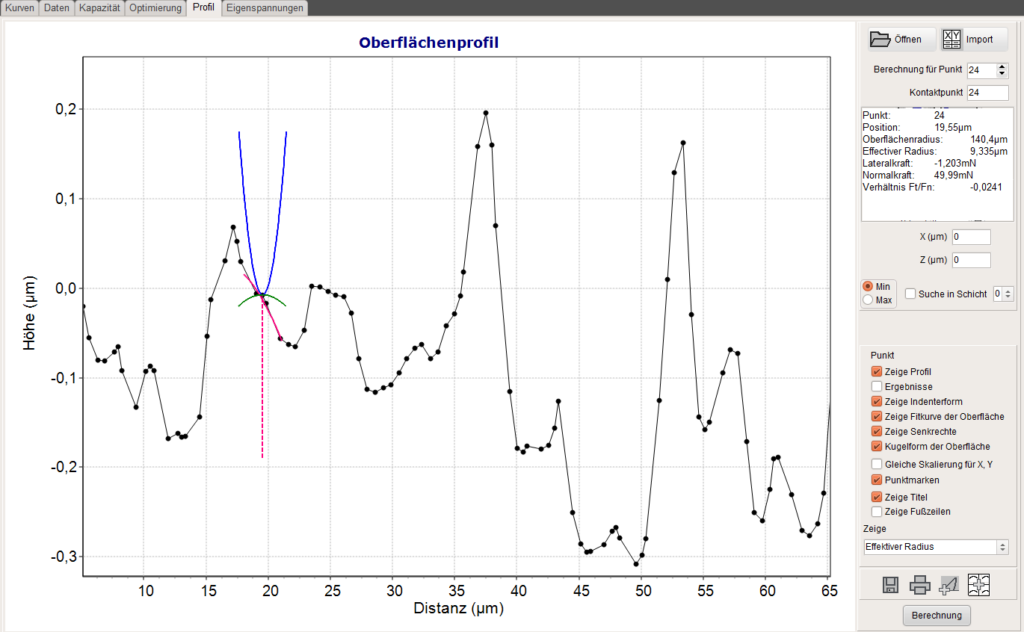
Der lokale Radius des Oberflächenabschnitts wird berechnet und ein effektiver Radius wird daraus abgeleitet. Die Oberflächenneigung bestimmt die Kraftkomponenten in senkrechter und lateraler Richtung und beide Kraftkomponenten werden zusammen mit dem effektiven Radius genutzt um die lokalen Spannung- oder Dehnungsfelder zu berechnen. Für scharfe Rauheitsspitzen und größere Radien der Abtastspitze kann der Kontaktpunkt von dem berechneten Punkt abweichen. Dies wird in der Berechnung berücksichtigt. Die Profil-Seite zeigt alle Kontaktdetails und die Spannungs- oder Dehnungsergebnisse.
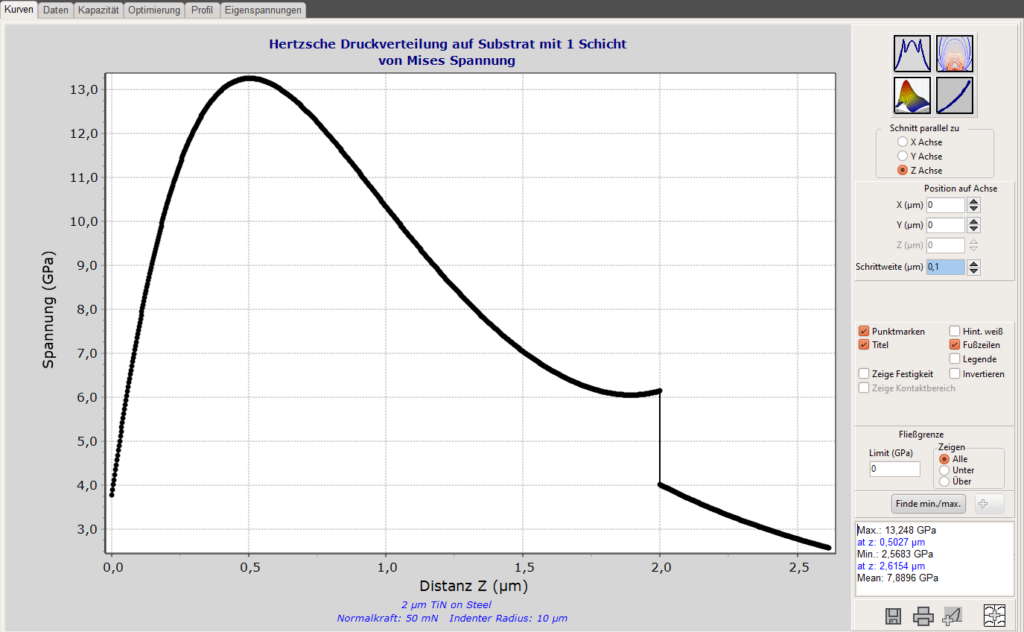
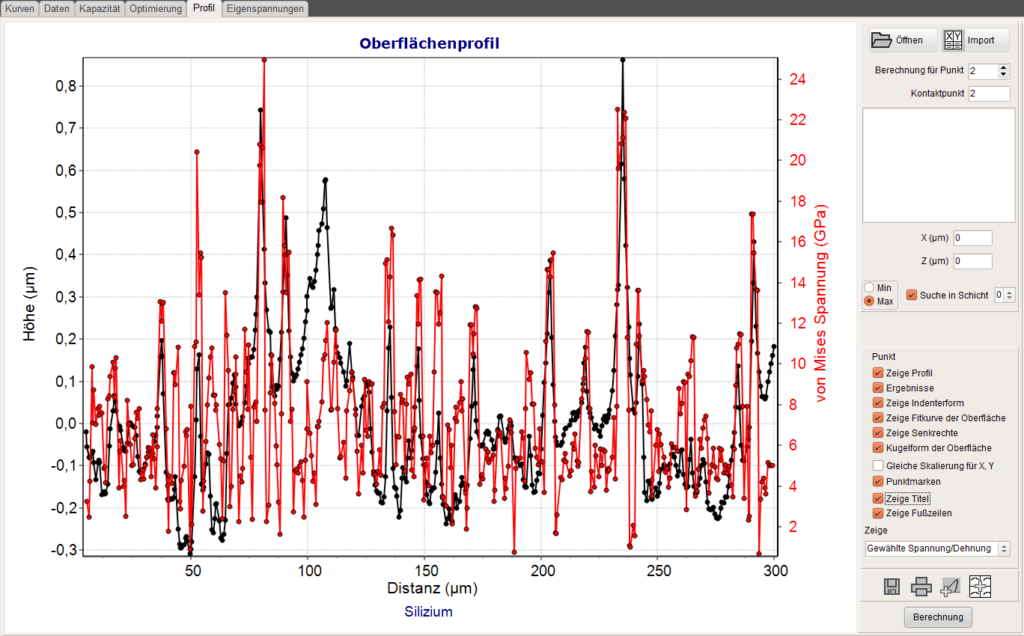
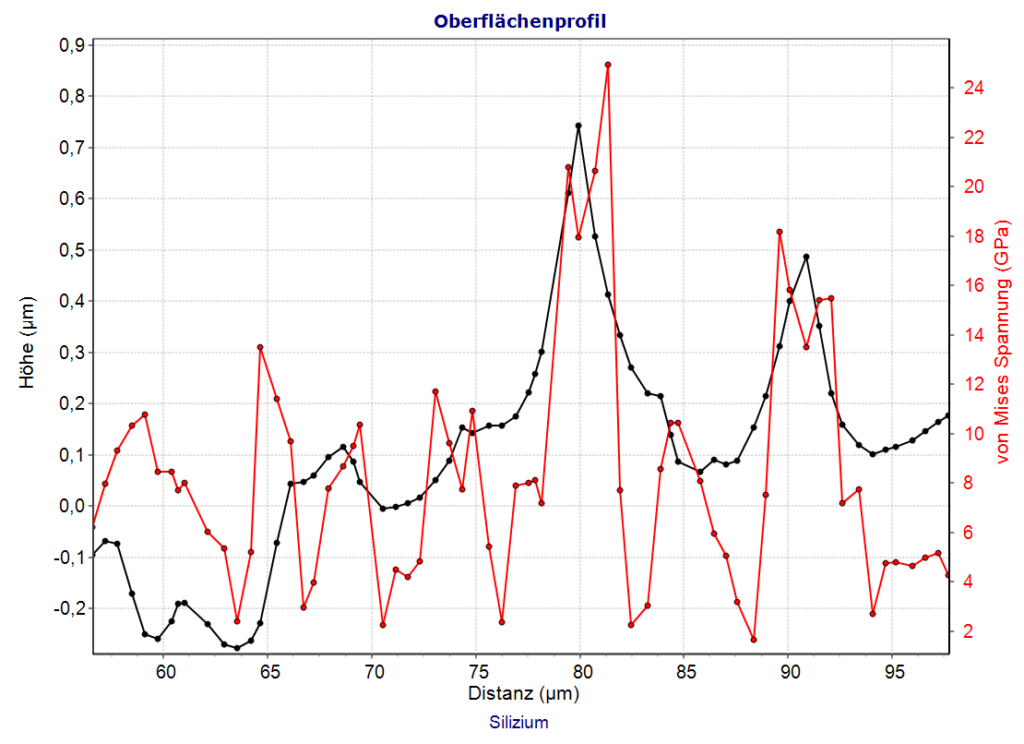
Nach Drücken der Berechnungs-Schaltfläche können die maximale oder minimale Spannung oder Dehnung in der ausgewählten Schicht oder dem Substrat für jeden Punkt des Profils angezeigt werden. Spannungsspitzen können so leicht identifiziert werden. Das wird in den folgenden Grafiken für die von Mises Spannung zusammen mit dem Höhenprofil dargestellt. Die Rechnung wurde für einen Indenterradius von 10µm auf einem Siliziumsubstrat für eine Kraft von 10mN durchgeführt.
Die Grafik zeigt des Oberflächenprofil zusammen mit der Form der kugelförmigen Spitze, dem Fit des lokalen Oberflächenprofils und dem lokalen Radius der Oberfläche im Kontaktpunkt. Die gestichelte Linie ist die Oberflächennormale. Durch die unterschiedliche Skalierung der beiden Achsen wird ihr Anstieg als auch die Form der Kugel verzerrt.
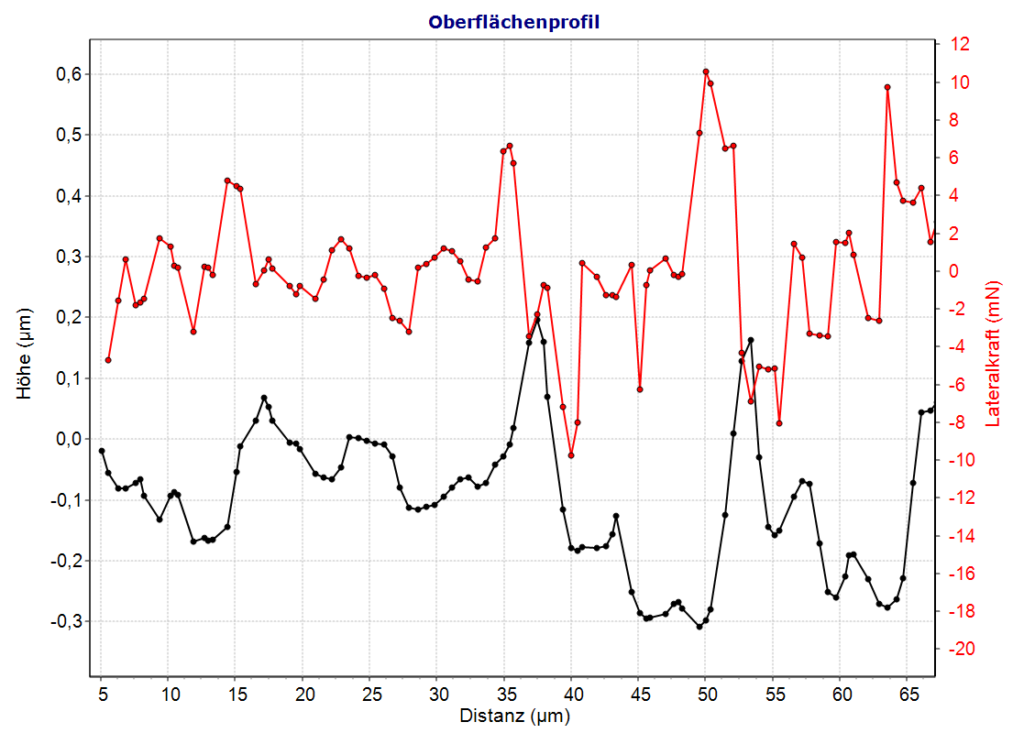
Durch die geneigte Oberfläche wird die Gesamtkraft in eine normale und laterale Komponente aufgespalten, die hier in der Grafik zu sehen ist. Bei positivem Anstieg ist die Lateralkraft positiv und sonst negativ.
Maximale von Mises Spannung in der Oberfläche einer unbeschichteten Siliziumprobe in Abhängigkeit von der Position entlang eines Rauheitsprofils
Download
Diese Software arbeitet nach der Installation nur als Testversion mit eingeschränkten Rechten.
Sie haben die Möglichkeit, eine zeitbegrenzte Freischaltung der Vollversion für einen Zeitraum von 30 Tagen von uns zu erhalten. Sie brauchen dazu nur auf unsere E-Mail Adresse im Welcome Fenster zu klicken und die fehlenden Angaben in der vorbereiteten E-Mail ergänzen.
Nach Erwerb der Software erhalten Sie einen zeitlich unbefristeten Zugangscode.